Adhesive models

In addition to hertzian models, adhesive models capture the effect of distance-dependent attractive force between particles. Adhesive models are usually mathematically rather complicated, extending the Hertz theory in some way. Usually the equations for \(\delta(a)\) and \(a(P)\) are provided, reflecting the typical use of adhesive models in microscopy fields. For DEM models, the relationship \(P(\delta)\) is needed. In some cases, the \(\delta(a(P))\) is not analytically invertible and solution must be sought by iteration which can have some performance impacts.

Symbols used for adhesive models, in addition to those introduced for Hertzian models) are:

\(\gamma\)	surface energy (in models with adhesion)
\(P_{na}\)	normal adhesive (also called “pull-off” or “sticking”) force
\(P_c\)	critical force (leads to surface separation); maximum tensile force an adhesive contact can sustain
\(\alpha\)	[COS99] transition parameter between DMT and JKR models
\(\hat\delta\)	reduced penetration (dimensionless)
\(\hat P\)	reduced total normal force (dimensionless)
\(\hat a\)	reduced contact radius (dimensionless)

[Mau92] introduced normalized (dimensionless) numbers of some quantities on adhesive contacts; they are useful for validating models against published plots regardless of the value of input parameters. These units are defined as follows:

\begin{align*} \hat a&=a\left(\frac{K}{\pi\gamma R^2}\right)^{\frac{1}{3}}, \\ \hat\delta&=\delta\left(\frac{K^2}{\pi^2\gamma^2 R}\right)^{\frac{1}{3}}, \\ \hat P&=P\frac{1}{\pi\gamma R}. \end{align*}

Derjaugin-Muller-Toporov (DMT)

The DMT model superposes adhesion outside of the area of contact as predicted by the Hertz model. The magnitude of adhesion is derived from surface energy \(\gamma\) using thermodynamic approach ([Mod13] pg 39; [DMT75] derives adhesion force for one surface with nonzero surface energy, here we suppose they have together the surface energy of \(2\gamma\)):

\[P_{na}=-4\pi R\gamma\]

which acts against (negative sign) the elastic repulsion of particles (eq); the total normal force then reads \(P_n=P_{ne}+P_{nv}+P_{na}\). Contact radius \(a\) can be expressed from (eq) by replacing \(P_{ne}\) with total normal force \(P_n\).

Todo

For completeness mention JKR model; mention Maugis model as the one which accounts for the transition between both, COS introducing the \(\alpha\) parameter, Schwarz (below) giving analytical solution.

Schwarz model

Schwarz [Sch03] proposes model which accounts for the DMT-JKR transition and, unlike the Maugis “Dugdale” model ([Mau92]), gives the \(a(F)\) and \(\delta(a)\) analytically. The surface energy is decomposed as short-range adhesion \(w_1\) and long-range adhesion \(w_2\), i.e.

(9)\[\gamma=w_1+w_2\]

and their proportion determines whether the model is DMT-like or JKR-like. The critical load is superposition of critical forces found in the JKR and DMT models respectively ([Sch03] (23)):

(10)\[P_c=-\frac{3}{2}\pi R w_1-2\pi R w_2.\]

DMT-JKR transition

For convenience, we will use the \(\alpha\in\langle 0\dots 1\rangle\) dimensionless parameter introduced by Carpick, Ogletree and Salmeron in [COS99] defined as ([Sch03] (34))

\[\alpha^2=-\frac{3 P_c+6\pi R \gamma}{P_c}\]

and by rearranging

(11)\[P_c=-\frac{6\pi R \gamma}{\alpha^2+3}.\]

Combining (9), (10) and (11) leads to

\[\gamma\left(\frac{-12}{\alpha^2+3}+4\right)=w_1\]

and by further rearrangements we can relate the ratio of short-range and long-range adhesion forces to \(\alpha\) both ways:

\[ \begin{align}\begin{aligned}\frac{w_1}{w_2}&=\frac{3(1-\alpha^2)}{4\alpha^2}\\\alpha^2=\frac{3}{4\frac{w_1}{w_2}+3}\end{aligned}\end{align} \]

We can see that extreme values of \(\alpha\) recover DMT (as limit) or JKR models, and intermediate values represent transition between them:

\(\alpha\)	\(w_1\)	\(w_2\)	model
→ 0	→ 0	\(\gamma\)	→ DMT
1	\(\gamma\)	0	JKR

Contact radius

Contact radius and force are related by the function ([Sch03] (36))

\[a=\left(\frac{R}{K}\right)^{\frac{1}{3}}\left(\alpha\sqrt{-P_c}\pm\sqrt{P_n-P_c}\right)^{\frac{2}{3}}\]

which is analytically invertible to

\[P_n=\left(\sqrt{a^3\frac{K}{R}}-\alpha\sqrt{-P_c}\right)^2+P_c.\]

The following plot shows both functions (dots are the inverse relationship; this plot appears in [Mau92], Fig. 5.):

(Source code, png, hires.png, pdf)

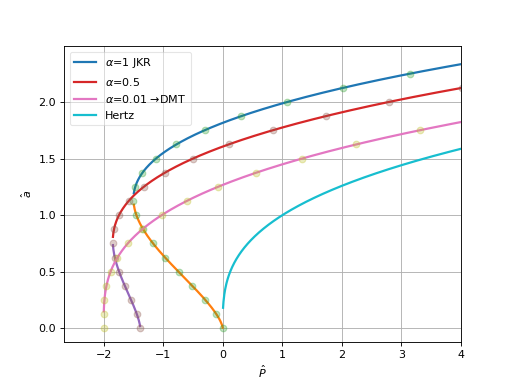
Peneration

Penetration is given as ([Sch03] (27))

(12)\[\delta=\frac{a^2}{R}-4\sqrt{\frac{\pi a}{3 K}\left(\frac{P_c}{\pi R}+2\gamma\right)}.\]

Plugging (11) into (12), we obtain

(13)\[\delta(a)=\frac{a^2}{R}-4\underbrace{\sqrt{\frac{2\pi\gamma}{3K}\left(1-\frac{3}{\alpha^2+3}\right)}}_{\xi}\sqrt{a}=\frac{a^2}{R}-4\xi\sqrt{a}\]

where the \(\xi\) term was introduced for readability. This equation is not analytically invertible and has to be solved numerically. We can find the global minimum as

\begin{align*} \delta'(a)&=\frac{2a}{R}-2\xi a^{-\frac{1}{2}} \\ \delta'(a_{\min})&=0 \\ a_{\min}&=(\xi R)^{\frac{2}{3}} \\ \delta_{\min}&=\delta(a_{\min})=-3R^{\frac{1}{3}}\xi^{\frac{4}{3}}. \end{align*}

The second derivative

\[\delta''(a)=\underbrace{\frac{2}{R}}_{>0}+\underbrace{\xi a^{-\frac{3}{2}}}_{\geq 0}>0\]

is strictly positive as \(\xi\), \(R\) and positive and \(a\) non-negative.

Given known penetration \(\delta\), we can find the corresponding value of \(a\) with Newton-Raphson or Halley’s methods. There are two solutions for all \(\delta\in(\delta_{\min}\dots 0\rangle\). The solution for the ascending branch (\(\delta'(a<a_{\min})>0\)) is energetically unstable and we can ignore it in dynamic simulations.

As the initial solution for iteration, we can use the (stable) value for zero overlap (satisfying \(\delta(a_0)=0\)) expressed from (13) as \(a_0=(4\xi R)^{\frac{2}{3}}\) for fresh contacts (where the overlap is likely close to zero); for previously existing contacts, the previous value of \(a\) is a good initial guess.

This plot shows both loading and unloading (unstable) branches, obtained via Newton iteration (bisection for the unstable branch for simplicity); this plot reproduces [Mau92], Fig. 6.:

(Source code, png, hires.png, pdf)

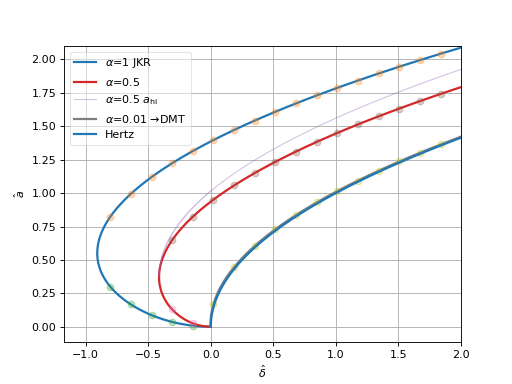
Note

Values bracketing possible solutions, \(a\in\langle a_{\mathrm{lo}}, a_{\mathrm{hi}}\rangle\) (lower and upper brackets) are to be defined for guarded iterative methods.

The lower bracket is

\[\begin{split}a_{\mathrm{lo}}=\begin{cases} a_{\min}=(\xi R)^\frac{2}{3} & \text{if $\delta<0$} \\ a_0=(4\xi R)^{\frac{2}{3}}=4^\frac{2}{3}a_{\min} & \text{if $\delta\geq0$} \end{cases}.\end{split}\]

The upper bracket \(a_{\mathrm{hi}}\) can be obtained from (13). Since \(\delta'(a)\) is bounded by

(14)\[\delta'(a)=\frac{2a}{R}-\underbrace{2\xi a^{-\frac{1}{2}}}_{\geq0}\leq\frac{2a}{R}=\delta_{\mathrm{Hertz}}'(a)\]

where \(\delta_{\mathrm{Hertz}}=a^2 R\) is the Hertz limit valid for \(\alpha\to0\); it is a purely geometrical relationship, valid also for the DMT model. It follows for the stable branch of \(a(\delta)\) that

\[\delta(a>a_{\min})\geq \delta_{\mathrm{Hertz}}(a-a_{\min})+\delta_{\min},\]

i.e. that \(\delta_{\mathrm{Hertz}}(a)\) with the origin shifted to \((a_{\min},\delta_{\min})\) is the lower bracket for \(\delta(a)\). Since \(\delta'(a)=1/a'(\delta)\) (as per derivative rule for inverses), the inequality (14) implies

\[a(\delta)\leq a_{\mathrm{hi}} = a_{\mathrm{Hertz}}(\delta-\delta_{\min})+a_{\min}=\sqrt{R(\delta-\delta_{\min})}+a_{\min}.\]

The upper bracket is shown in the plot above for \(\alpha=0.5\).

By composing \(P_n(a)\) and (numerically evaluated) \(a(\delta)\), we obtain the displacement-force relationship ([Mau92], Fig. 7.)

(Source code, png, hires.png, pdf)

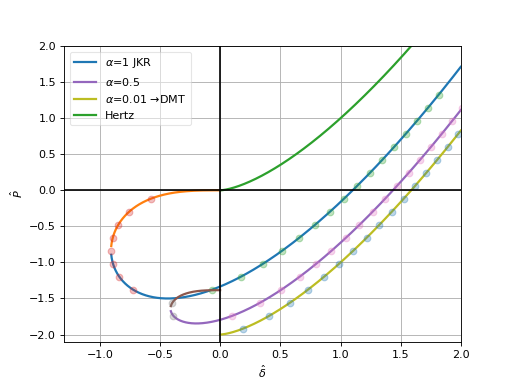
Implementation note:

DMT/Schwarz contact models can be used via woo.dem.Law2_L6Geom_HertzPhys_DMT, when woo.dem.Cp2_FrictMat_HertzPhys.gamma (surface energy \(\gamma\)) is non-zero; woo.dem.Cp2_FrictMat_HertzPhys.alpha (Carpick-Ogletree-Salmeron transition parameter \(\alpha\)) determines the model behavior on the continuous DMT (\(\alpha=0\)) – JKR (\(\alpha=1\)) range. Appropriate engines are returned from woo.dem.DemField.minimalEngines when model is an instance of woo.models.ContactModelSelector with name equal to "DMT" or "Schwarz".

Tip

Report issues or inclarities to github.